more content in German | mehr Inhalt auf deutsch
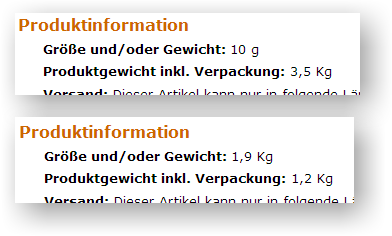
Translation: “Product size and/or weight” in first black line and “Shipping weight” (product+packaging) in second.
Which do you want – an extremely heavy packaging or one with negative weight?
(Two third-party’s offers on Amazon.de in Feb 2009)
Links of the Week (2009/03)
- Spontis’s Top 10 of the most extraordinary female singers (part 1, part 2; German, but with videos).
- Several Simpsons movie references.
- Again phantastic photos at The Big Picture, this time Earth from space.
- How much are a million pennies? Or a trillion? Or…? The MegaPenny Project helps to understand these numbers (to some extent)… (via Bad Astronomy).
Calculating weekdays in your head
Since this topic briefly came up during my “mini class reunion” at Christmas, I thought I’d post it here, too, how you can calculate a weekday in your head.
Note: modulo (short: mod) means the remainder of a division of two numbers (e.g. 15 modulo 7 = 1, because 15 = 2·7 + 1), which I will use here for the sake of brevity. The resulting values correspond to the days of the week, hence 7, of course.
We’ll use 20 Nov 2011 as an example. It won’t work without calculation and memorizing, though:
- Take the year since 1900 modulo 7. Example: 2011–1900 = 111; 111 mod 7 = 6.
Hint: You can subtract 70 for starters (or any other multiple of 7) to make it easier; the remainder of the division won’t change because of this, of course. - Due to the leap years, you then add the integer part of one quarter of the years since 19001, in our example ⌊111:4⌋ = 27. And take the remainder of this number too2: 27 mod 7 = 6.
Hint: Of course it’s 100:4 = 25 for the year 2000, which you can use as an easy-to-remember basis.
Hint: You can also calculate with -1 instead of 6, since that results in the same value in the end, thanks to modulo 7. - For the month, you memorize this table (which denotes the variations in the weekday for the first days of the months):
Jan–Mar 0 3 3 Apr–Jun 6 1 4 Jul–Sep 6 2 5 Oct–Dec 0 3 5 In the example: 3 for November.
Hint: It’s probably easiest memorized as row 0-3-3, column 0-6-6-0 and sub-columns 1-2-3 4-5-5(!).
(I think it would work without such a table, too, but once you got it memorized, I guess it’s easier this way.) - If the date in question is in January or February of a leap year, subtract 1. (Don’t forget!)
- Then simply add the day, in the exaple 20. Or straight away the value modulo 7, here 6.
- The sum modulo 7 then results in a value from 0 to 6, with 0 for Sunday, 1 for Monday, …, 6 for Saturday.
Our example thus results in 6+6+3+20 = 35; 35 mod 7 = 0, so 20 Nov 2011 is a Sunday.
If you used -1 instead of 6: 6-1+3-1 = 7; 7 mod 7 = 0 or -1-1+3-1 = 0.
Quite easy, isn’t it? 
Photo: aidasonne – Fotolia.com
The perfect post
The Holy Trinity of the Three Sevens in the combination of mind and soul with the four elements brings you this divine perfect post, the sevenhundredandseventyseventh of my blog, for your complete enlightenment.
Know ye, it is written:
Divide the triple bad luck twice by the elemental bad luck, so that it shall dissolve itself and the divine perfect remain.1
Like the trinity and the four elements put together result in the Seven, the perfect 777 consists of four elemental trinities based on the double Three.2
Write this following Prayer in your best handwriting on handmade paper, frame it and hang it 7.77 centimeters above the floor, lie down in front of it at a distance of 7.77 inches and loudly speak the Prayer 777 times in 7.77 hours, so that you shall find complete enlightenment and no longer need candles nor lightbulbs, now and for evermore.
This is how ye shall pray:
Our number, who art in cosmos,
Hallowed be thy prime factors.
Thy factorization come.
Thy calculation be done,
In the computer as in our heads.
Give us this day our daily enlightenment.
And forgive us our miscalculations,
As we forgive those who calculate against us.
And lead us not into division by zero,
But deliver us from the 666.
For thine is the 3, and the 7, and the 37,
for ever and ever.
Amen.
Percentage calculation problems or The shrunken bodies
Statista is always worth a look if you’re no statistics hater (and speak German). Today’s stats of the day about the question “How tall are you?” (» filtered by sex), and 22358 adult Germans had been asked.
The unfiltered overview shows 2.9% for the really big ones (to which I also belong, thanks to my 190 cm), rounded on top of the bars for clarity:
(190 cm and taller: 2.9%)
You can also enter a number to compare to – and the result is:
Your reply: 190.0 cm
98.0% are smaller than 190 cm.
2.0% are like you taller than 190 cm.
Oops, did 0.9% of the people suddenly shrink? Or how else could this result be explained then? And why “are like you taller than 190 cm”?
If I enter 189 cm for testing purposes, I get: “96.8% are smaller than you. 3.2% are taller than you.” So nobody is 189 cm tall? Are 0.3% 189 cm tall and 2.9% taller, or 1.2% 189 cm and 2.0% taller? For 154 cm, the numbers “2.2%/97.8%” are reported, basically matching the bar graph, but here, too, with the words “smaller” and “taller” without mentioning the size of exactly 154 cm.
Well, apparently there’s room for improvement… but the title still says “BETA”. Let’s see if the error report that I sent them (they got a special link for that) will have any effect.
