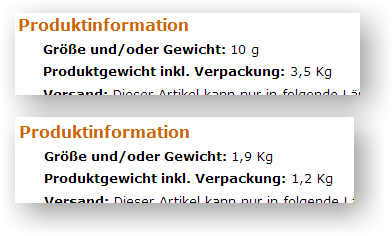
Was darf’s sein – eine extrem schwere Verpackung oder eine mit negativem Gewicht?
(Zwei Drittanbieter-Angebote bei Amazon.de im Feb. 2009)
 …oder: Wie eine Wahrsagerin schon am Kalender scheitert. Es geht um die Glaskugelglotzerin mit Schweizer Postfachadresse (in CH-8107 Buchs), die in den letzten Wochen fleißig inseriert hat, u.a. in der Hörzu, großspurig titelnd: „Weltweite Krise: Maria Esmeralda hat beschlossen zu reagieren“.
…oder: Wie eine Wahrsagerin schon am Kalender scheitert. Es geht um die Glaskugelglotzerin mit Schweizer Postfachadresse (in CH-8107 Buchs), die in den letzten Wochen fleißig inseriert hat, u.a. in der Hörzu, großspurig titelnd: „Weltweite Krise: Maria Esmeralda hat beschlossen zu reagieren“.
Sie nennt sich „eine der erfolgreichsten und erfahrensten Hellseherinnen der Welt“, hat aber anscheinend weder eine eigene Website noch einen Wikipedia-Eintrag, nur o.g. Postfachadresse; sie will sich nach „über 35 Jahren Erfahrung“ zurückziehen, nur eben noch schnell 500 Menschen (die sich bis 31.12. hätten melden sollen) ach so großzügig beschenken: Mit „13 persönlichen Ereignis-Daten“, „goldenen Glückszahlen, ohne die kein Gewinn möglich ist“, und ihrem „berühmten Glücksbringer“ – über den man nichts im Netz findet. Warum jetzt? Sie meint:
2009 ein außergewöhnliches Jahr
[…] Es wird durch 3 außergewöhnliche Ereignissen gekennzeichnet.
1) 2009 gibt es drei Freitage, die auf einen Dreizehnten fallen. Das heißt, es gibt drei einzigartige Gelegenheiten, um eine große Geldsumme zu gewinnen!
Ersteres stimmt. Letzteres ist ihre außergewöhnliche Interpretation eines im allgemeinen Aberglauben eher als Unglückstag gesehenen Datums. (Übrigens in deutscher Rechtschreibung, in der Schweiz gibt’s kein „ß“. Aber das muss ja nichts bedeuten…)
2) 2009 gibt es in zwei aufeinander folgenden Monaten, im Februar und im März, jeweils einen Freitag, den Dreizehnten. Dieses Phänomen tritt nur einmal im Jahrhundert auf und begrenzt einen Zeitraum, in dem uns das Glück außergewöhnlich hold ist. Man muss jedoch über diese Tatsachen informiert sein und in der Lage sein, von dieser sich bietenden Gelegenheit zu profitieren.
Man sollte annehmen, wer so eine Aussage (Hervorhebung von mir) über solch eine Besonderheit trifft, der hat sie auch überprüft. Tatsache ist aber: Diese Freitagskonstellation tritt auch in den Jahren 2015, 2026, 2037, 2043, 2054, 2065, 2071, 2082, 2093 und 2099 auf (und auch elfmal im letzten Jahrhundert). Ich sehe da drei Möglichkeiten:
Der Vollständigkeit halber will ich euch ihr drittes „außergewöhnliche Ereignis“ nicht vorenthalten:
3) Außerdem ist 2009 auch ein einzigartiges Datum. Der 9. September 2009 schreibt sich in der Numerologie 9/9/9 oder auch 0 unendlich. Für die Chinesen ist dies das Jahr mit den besten Vorzeichen. Die 9 ist das Symbol für Glück und Stärke. Daher wird die Ziffer 9 auch immer durch den Drachen symbolisiert. Er hat 117 Schuppen (1+1+7=9), 81 männliche Schuppen (9×9 oder 8+1) und 36 weibliche Schuppen (9×4 oder 3+6), er vereinigt die Merkmale von 9 Wesen in sich, und der Drache hat 9 Kinder. Dies kündigt ein neues Leben voller Glück an, vorausgesetzt dass Sie die Schlüssel dafür besitzen.
„0 unendlich“? Dann ist die Numerologie noch dämlicher, als ich dachte… und das trotz all der konstruierten chinesischen Zahlenphantasterei, die hier wohl einfach beeindrucken soll.
Dass im chinesischen Aberglauben die 4 durch ihre klangliche Ähnlichkeit mit dem Wort für Tod als Unglückzahl gilt, verschweigt sie lieber, denn das wäre ja schlecht für ihre Dreizehner-Euphorie – wo doch die Quersumme 1+3=4 ist. Bullshit eben… als den man auch die Wahrsagerei insgesamt betrachten muss, solange es keine Beweise gibt, die für sie sprechen – und die gibt es eben nicht.
Siehe auch:
Liebe(r) Leser(in), hast Du diese Geschenke angefordert und bereits erhalten? Sind sie zufriedenstellend, gab es weitere Angebote, oder willst Du sonst etwas dazu sagen? Dann veröffentliche doch weiter unten auf dieser Seite einen Kommentar!
![]() Update: Wie erwartert, soll zum „richtigen“ Glück noch Geld gezahlt werden, sei es ein Buch oder sonstwas – siehe Kommentare unten (vielen Dank dafür). Also: Vergesst den teuren Kram von dieser Möchtegern-„Wahrsagerin“, die angeblich von jedem geträumt haben will – da kommt nichts Vernünftiges dabei raus!
Update: Wie erwartert, soll zum „richtigen“ Glück noch Geld gezahlt werden, sei es ein Buch oder sonstwas – siehe Kommentare unten (vielen Dank dafür). Also: Vergesst den teuren Kram von dieser Möchtegern-„Wahrsagerin“, die angeblich von jedem geträumt haben will – da kommt nichts Vernünftiges dabei raus!
![]() Update 21.8.09: Neues über Maria Esmeralda, ihre Homepage und möglicherweise eine bessere Kontaktmöglichkeit als die Postfachadresse.
Update 21.8.09: Neues über Maria Esmeralda, ihre Homepage und möglicherweise eine bessere Kontaktmöglichkeit als die Postfachadresse.
 Da das Thema kurz bei meinem weihnachtlichen „Mini-Klassentreffen“ aufkam, dachte ich, ich könnte es auch mal hier erwähnen, wie man im Kopf einen Wochentag berechnen kann…
Da das Thema kurz bei meinem weihnachtlichen „Mini-Klassentreffen“ aufkam, dachte ich, ich könnte es auch mal hier erwähnen, wie man im Kopf einen Wochentag berechnen kann…
Vorbemerkung: modulo (kurz: mod) bezeichnet den Rest einer Division zweier ganzer Zahlen (z.B. 15 modulo 7 = 1, da 15 = 2·7 + 1), was ich der Kürze wegen hier verwenden werde. Die entstehenden Werte entsprechen natürlich den Wochentagen, deshalb 7.
Als Beispiel nehmen wir den 20.11.2011. Ganz ohne Rechnen und Merken geht’s natürlich nicht:
| Jan–Mär | 0 | 3 | 3 |
| Apr–Jun | 6 | 1 | 4 |
| Jul–Sep | 6 | 2 | 5 |
| Okt–Dez | 0 | 3 | 5 |
Im Beispiel: 3 für den November.
Tip: Am einfachsten merkt man sich’s wohl als Zeile 0-3-3, Spalte 0-6-6-0 und Teil-Spalten 1-2-3 4-5-5(!).
(Es ginge an sich auch ohne eine solche Tabelle, aber wenn man sie sich mal gemerkt hat, ist es m.E. so einfacher.)
Ist doch ganz einfach, oder? ![]()
Foto: aidasonne – Fotolia.com
Die Heilige Dreifaltigkeit der Drei Sieben in der Verbindung von Geist und Seele mit den vier Elementen bringt Euch diesen göttlich vollkommenen Beitrag, den siebenhundertsiebenundsiebzigsten meines Blogs, zu Eurer vollkommenen Erleuchtung.

Wisset, es steht geschrieben:
Teilet das dreifache Unglück zwei Mal durch das elementare Unglück, auf dass es sich auflöse in Wohlgefallen und das göttlich Vollkommene übrigbleibe.1
So wie die Dreieinigkeit und die vier Elemente zusammen die Sieben ergeben, so bestehet die vollkommene 777 aus vier elementaren Dreieinigkeiten zur Basis der doppelten Drei.2
Schreibet das folgende Gebet in Eurer schönsten Schönschrift auf handgeschöpftes Papier, rahmet es und hänget es 7,77 Zentimeter über dem Boden an Eure Wand, leget Euch davor im Abstande von 7,77 Zoll, und sprechet das Gebet 777 Mal in 7,77 Stunden laut, auf dass Ihr findet vollkommene Erleuchtung und nicht benötigen werdet Kerzen noch Glühbirnen, jetzt und immerdar.
So sollet Ihr beten:
Zahl unsere im Kosmos,
geheiligt werden Deine Primfaktoren.
Deine Zerlegung komme.
Deine Berechnung geschehe,
wie im Computer, so im Kopfe.
Unsere tägliche Erleuchtung gib uns heute.
Und vergib uns unsere Rechenfehler,
wie auch wir vergeben unseren Taschenrechnern.
Und führe uns nicht in die Division durch Null,
sondern erlöse uns von der 666.
Denn Dein ist die 3 und die 7 und die 37
in Ewigkeit.
Amen.
Siehe auch: